Сложение дробей
При сложении дробей могут встретиться разные случаи.

Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.

Пример.
 

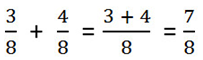
C помощью букв это правило сложения можно записать так:
 

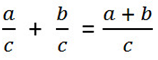
•     Записывая ответ, проверьте нельзя ли полученную дробь сократить.

Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться следующими правилами.

1.    Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти наименьшее общее кратное знаменателей.

Пример. Сложить дроби.
 

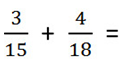
Как найти общий знаменатель
Находим НОК (15, 18).

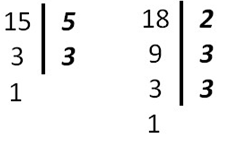
 НОК (15, 18) = 3 • 2 • 3 • 5 = 90

2.    Найти дополнительные множители для каждой дроби. Для этогонаименьший общий знаменатель (НОК из пункта 1) делим по очереди на знаменатель каждой дроби. Полученные числа и будут дополнительными множителями для каждой из дробей. Множители записываем над числителем дроби справа сверху. 

90 : 15 = 6 - дополнительный множитель для дроби 3/15.

90 : 18 = 5 - дополнительный множитель для дроби 4/18.

 
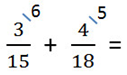
3.    Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь основным свойством дроби.После умножения в знаменателях обеих дробей должен получиться наименьший общий знаменатель. Затем складываем дроби как дроби с одинаковыми знаменателями. 

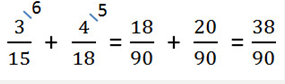
4.    Проверяем полученную дробь.
-   Eсли в результате получилась неправильная дробь, результат записываем в виде смешанного числа. Проверим нашу дробь. 38 < 90 У нас дробь правильная.
-  Если в результате получилась сократимая дробь, необходимо выполнить сокращение. 

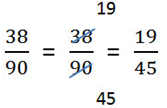
5.    Ещё раз весь пример целиком. 

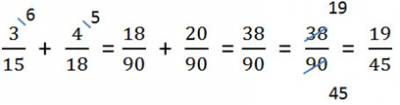
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.

Чтобы сложить смешанные числа нужно.
1.    Отдельно сложить их целые части.
Пример.
 

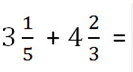
Складываем целые части.
3 + 4 = 7

2.    Отдельно сложить дробные части.

Если у дробных частей знаменатели разные, то сначала приводим их к общему знаменателю, а затем складываем.
 

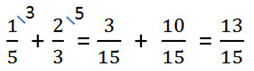
3.    Сложить полученные результаты из пунктов 1 и 2. 

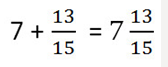
4.    Если при сложении дробных частей получилась неправильная дробь, то нужно выделить целую часть из этой дроби и прибавить к полученной в пункте 1 целой части.

Ещё один пример на сложение дробей.
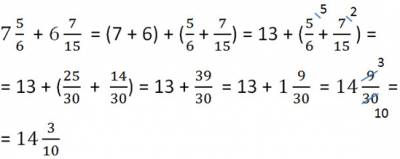