Вычитание дробей
При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Пример.
 

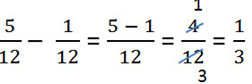
•     Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.

В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так:
 
 

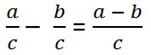
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Пример.
 
Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную дробь 7/7 и вычитают по правилу вычитания дробей с одинаковыми знаменателями.
 
 

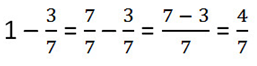
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа.
 

Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.
 

Пример.
 
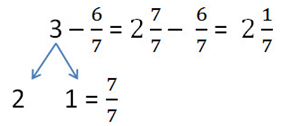
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
 

Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
При подобных расчётах могут встретиться разные случаи.
 

Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого (что вычитаем).
Пример.
 
 

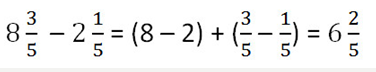
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
 

В этом случае вначале нужно привести к общему знаменателю дробные части, а затем выполнить вычитание целой части из целой, а дробной из дробной.
Пример.
 
 

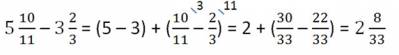
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример.
 
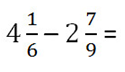
Так как у дробных частей разные знаменатели, то как и во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.
 
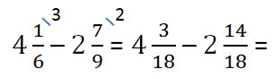
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
3 < 14 

Поэтому, вспомнив вычитание правильной дроби из целого числа, займём единицу из целой части и представим эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.
 
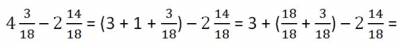
Сложим полученную неправильную дробь 18/18 и дробную часть уменьшаемого и получим:
 
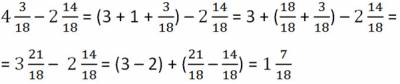
Все рассмотренные случаи можно описать с помощью правил вычитания смешанных чисел.
•    Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
•    Если дробная часть уменьшаемого меньше дробной части вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю.
•    Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
•    Вычитаем из целой части целую, а из дробной - дробную.
•    Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.