Длина окружности
Возьмем циркуль. Установим ножку циркуля с иглой в точку O, а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют -окружность.
 

Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
 
•    (•) O - называется центром окружности.
•    Отрезок, который соединяет центр и любую точку окружности, называется радиусом окружности. Радиус окружности обозначается буквой R. На рисунке выше - это отрезок OA.
•    Отрезок, который соединяет две точки окружности и проходит через её центр, называется диаметром окружности. Диаметр окружности обозначается буквой D. На рисунке выше - это отрезок BC. 
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение D = 2R.

Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π(читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
    

• Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
• π≈3,14...

Число «Пи» относится к числам, точное значение которых записать невозможно ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам для наших вычислений достаточно использовать значение π, 
округленное до разряда сотых π≈3,14... .
Теперь, зная, что такое число π, мы можем записать формулу длины окружности.
    

• Длина окружности - это произведение числа π и диаметра окружности. Длина окружности обозначается буквой С (читается как «Це»). 
• C = πD
• C = 2πR, так как D = 2R

Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число πокруглите до сотых.
Воспользуемся формулой длины окружности: 

C = 2πR ≈ 2 • 3,14 • 24 ≈ 150,72 см

Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14).
Выразим из формулы длины окружности диаметр. 

C = πD 
D = С / π 
D = 56,52 / 3,14 = 18 дм
 

Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки A и B. Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга AB и черная дуга AB. Точки A и B называют концами дуг.
Соединим точки A и B отрезком. Полученный отрезок называют хордой.
 
    

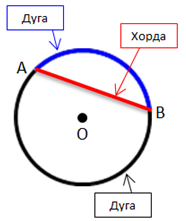
• Точки A и B делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга AB. 
• Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
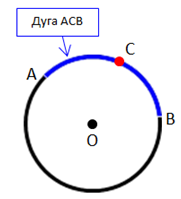